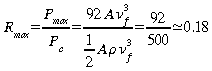
Capsule hydrologie
Martin Aubé
Collège de Sherbrooke
01/2003
Voici quelques équations qui permettent de modéliser l'écoulement de l'eau dans un cours d'eau.
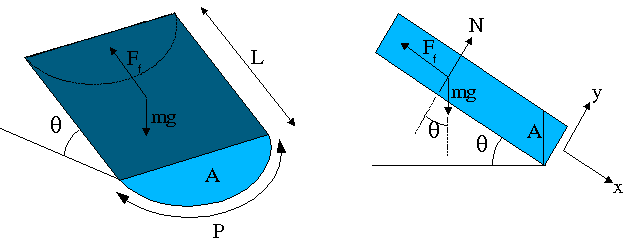
Figure 1: Diagramme des forces agissant sur un élément d'eau dans une rivières idéalisée.
Selon la 2e loi de Newton en supposant un état d'équilibre dynamique car la vitesse d'écoulement est constante:
donc selon x:
La force de frottement provient du mouvement turbulent entre l'écoulement et la granulosité du lit de la rivière.
Nous pouvons aussi montrer que
d'où
Ce qui implique que:
où V= élément de volume d'eau
De cette dernière équation, nous pouvons isoler la vitesse d'écoulement:
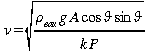
En hydrologie, on définit le coefficient de Chezy (c) comme:
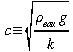
ainsi que le rayon hydraulique (R) comme le rapport de l'aire d'écoulement (A) que divise la longueur de contact entre l'eau et le lit du cours d'eau (P).
d'où
pour des angles petits (inférieurs
à ~5o),
et
où m est la pente du terrain dans la direction de l'écoulement nous pouvons simplifier l'expression de la vitesse d'écoulement.
La valeur du coefficient de Chezy peut être calculé à l'aide de l'équation empirique ci-dessous.
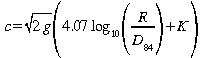K = {2, ..., 4.24}
D84 est le diamètre d'agrégats du fond de la rivière pour lequel 84% des agrégats ont un diamètre inférieur à D84.
|
Ex.: Soit une rivière de 5 m de largeur et de 2m de profondeur au centre et avec P épousant une forme triangulaire avec le maximum de profondeur au centre et dont la pente dans le sens de l'écoulement est de 2% (m=0.02). Nous supposerons que D84=3 x 10-3 m (à justifier) . Calculez la vitesse d'écoulement de l'eau. Dans
ce cas, A= 2.5 m x 2 m = 5 m2 et
Nous prendrons K=2 (à justifier)
|
Références:
Gray, D. M., Manuel des Principes d'Hydrologie, Pub. du Secrétariat, Comité national canadien de la Décennie hydrologique internationale, 1972
La force de frottement
exercée sur un objet se déplançant à la
vitesse
dans
un écoulement d'un fluide se déplaçant à
la vitesse
est
donné par l'équation ci-dessous:
où 
=
coefficient de frottement fluide qui dépend de la forme et de
la texture de l'objet
=
masse volumique du flude (1000 kg/m3 pour l'eau),
=
section de l'objet perpendiculaire à la direction de la
vitesse relative
Voici un tableau de
valeurs de
pour
quelques formes communes:
|
Forme |
|
|---|---|
|
Plaque mince |
1,28 |
|
Sphère
|
0,47 |
|
Demi-sphère
|
0,42 |
|
Cube
|
1,05 |
|
Cube tourné
|
0,8 |
|
Cône
|
0,5 |
|
Cylindre court
|
1,15 |
|
Cylindre long
|
0,82 |
|
Goutte
|
0,04 |
|
Demi-goutte
|
0,09 |
|
Balle de fusil |
0,3 |
Considérons maintenant le mouvement d'une plaque mince faisant office de pale fixée sur tambour cylindrique dont l'axe de symétrie est parallèle à la surface d'un cours d'eau mais perpendiculaire à la direction de l'écoulement. Si nous considérons que cet axe correspond à un axe de rotation et que ce dernier est ammaré à la terre ferme de sorte que le tambour est mis en rotation par le courant. La force exercée sur une plaque par le frottement fluide est donnée par:
La puissance mécanique associée au mouvement de cette plaque sous l'action de la force de frottement est donnée par:
Si nous dérivons cette expression pour l'égaler à 0 nous obtenons les minimums et maximums qui correspondent à
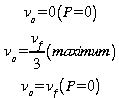
La puissance maximale est atteinte lorsque la plaque se déplace au tiers de la vitesse de l'écoulement.
Il est dès lors possible de déterminer la puissance mécanique maximale produite par ce type de turbine.
Durant une seconde, le
volume d'eau qui se serait écoulée librement à
travers une surface imaginaire de grandeur A est données par
le produit
et
donc la masse correspondante par unité de temps est donnée
par
La puissance totale disponible provient de l'énergie cinétique équivalente:
L'efficacité de récupération de la puissance mécanique disponible est donc donnée par:
et donc
