Champ magnétique![]() [tesla]
= [T] = [(N s) / (C m)] ou [Gauss] = [10-4 T] [8.1]
[tesla]
= [T] = [(N s) / (C m)] ou [Gauss] = [10-4 T] [8.1]
dipôle vs monopôle magnétique
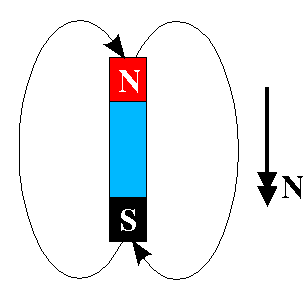
lignes de champ magnétique (dans la direction où pointe le pôle nord de l'aiguille d'une boussole)
Capsule magnétostatique
Martin Aubé
Collège de Sherbrooke
02/2003
Note: le sections équivalentes dans le volume Physique II: Électricité et magnétisme de Benson sont marqués de noir.
Champ magnétique![]() [tesla]
= [T] = [(N s) / (C m)] ou [Gauss] = [10-4 T] [8.1]
[tesla]
= [T] = [(N s) / (C m)] ou [Gauss] = [10-4 T] [8.1]
dipôle vs monopôle magnétique
lignes de champ magnétique (dans la direction où pointe le pôle nord de l'aiguille d'une boussole)
Force de Lorentz: On définit le champ magnétique en fonction de sont effet sur la matière chargée électriquement. [8.1]
![]() L'orientation
de la force est données par la règle de la main droite
L'orientation
de la force est données par la règle de la main droite
Comme la force est ^ à la vitesse, elle ne fait aucun travail et ne peut donc pas être responsable d'un changement d'énergie cinétique de la particule chargée.
Si B est constant, et comme la grandeur de la vitesse est aussi constante, la force est constante et radiale (F u r) on peut donc l'assimiler à un mouvement circulaire.
Ainsi
![]()
![]()
Force magnétique exercée sur un conducteur parcouru par un courant (ici B ^ au fil) [8.2]
![]() comme
comme
![]() on
peut écrire
on
peut écrire
![]() et
de façon générale pour une orientation
quelconque du fil par rapport au champ:
et
de façon générale pour une orientation
quelconque du fil par rapport au champ:
![]()
Moment de force magnétique exercée sur une boucle de courant:
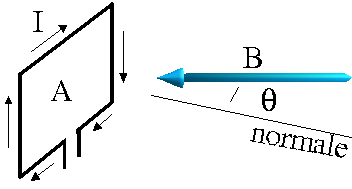
![]() ou
N= nombre de tours et M = moment de force
ou
N= nombre de tours et M = moment de force
![]()
de façon plus générale:
![]()
Application: moteur
Mouvement hélicoïdal
Aurores boréales [8.5]
bouteille magnétique
Cyclotron: champ magnétique et électrique combiné [8.7] [8.8]
![]()
![]()
![]()
Source de champ magnétique
Fil (infini) parcouru par un courant électriquement (résultat empirique)
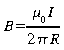 m0=perméabilité
du vide = 4 p x 10-7
T.m/A [9.1]
m0=perméabilité
du vide = 4 p x 10-7
T.m/A [9.1]
B est circulaire centré sur le fil pour toute distance du fil R
Calcul de la force entre deux fils parallèles [9.2]
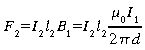 d
= distance entre les fils
d
= distance entre les fils
La force par unité de longueur est donc donnée par
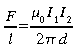
Selon Laplace, si B pour un fil infini est en 1/R, ceci implique que dB créé par un élément infinitésimal de fil varie en 1/R2
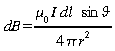 (loi
de Biot-Savart) ou
(loi
de Biot-Savart) ou
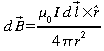 [9.3]
[9.3]
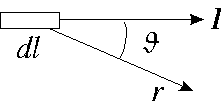
l'angle ê est défini comme l'angle entre le courant et le vecteur r qui relie l'élément de fil dl et le point de détermination du champ.
Champ magnétique d'une boucle de courant de rayon a
Si on intègre dB pour une boucle de courant nous pouvons trouver le champ au centre de cette dernière.
Dans ce cas, sin ê =1 et r est constant et égal à a . L'intégrale se ramène donc simplement à intégrer dl sur le cercle ce qui vaut 2 à r, d'où
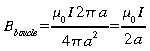
De façon générale,
![]()
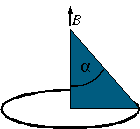
![]() N boucles superposées
N boucles superposées
Solénoïdes
Le solénoïde est un dispositif constitué de N spires de fil enroulées selon la forme d'un cylindre. Le champ magnétique sur l'axe de symétrie est donné par:
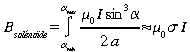 où
s=nombre de spires par mètre
où
s=nombre de spires par mètre
À l'extérieur du solénoïde le champ est presque nul (expliquer avec la main droite I, r, ou argumenter avec le fait que s'il n'est pas nul à l'extérieur il doit être non nul partout)
Définition du moment magnétique dipolaire
![]() l'orientation
du vecteur unitaire est donnée la direction du pouce en
refermant les autres doigts de la main droite dans le sens du
courant dans une boucle. [8.3]
l'orientation
du vecteur unitaire est donnée la direction du pouce en
refermant les autres doigts de la main droite dans le sens du
courant dans une boucle. [8.3]
Théorème d'Ampère
![]() I
étant le courant net traversant la surface délimitée
par le parcours.
I
étant le courant net traversant la surface délimitée
par le parcours.
Ex: le fil infini Si on choisit une parcours circulaire centré sur le fil et dont la normale est parallèle au fil, B est // à dl et on peut écrire:
![]()
d'où
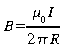 tel
que déjà vu.
tel
que déjà vu.
Démontrer Bsolénoïde avec le théorème d'Ampère
Énergie potentielle d'un dipôle magnétique dans un champ magnétique [8.3]
![]()
on peut aussi exprimer le moment de force sur le dipôle comme:
![]() (rappelons que
(rappelons que
![]() )
)
Comme la présence d'un moment de force net conduit à une rotation du système, le moment dipolaire sera stable lorsqu'il sera orienté dans la direction du champ et donc un moment de force nul. Comme cette condition correspond à la stabilité maximale, elle est rencontrée simultanément à l'énergie minimale.