Théorie cinétique des gaz

Martin Aubé Ó

12 janvier 2004

L'ensemble de la thermodynamique repose sur l'idée qu'un système peut être caractérisé par un ensemble limité de variables macroscopiques (température (T), pression (P), concentration (N)). Cette idée s'appuie sur l'hypothèse que toutes les particules composant le fluide sont identiques. Toutefois cette idée et donc la thermodynamique n'est valide que lorsque le système est dit en équilibre thermodynamique. C'est-à-dire que ces variables sont uniformes et constantes dans le volume considéré. La thermodynamique est très puissante puisqu'elle permet de décrire simplement le comportement de systèmes extrêmement complexes.

Pour bien comprendre l'origine de cette théorie ainsi que la signification des variables macroscopiques il convient de passer à l'échelle microscopique. Nous considérerons le cas d'un gaz parfait constitué d'un très grand nombre de particules identiques. Remarquez que le terme « particule » est ici très large puisque cette théorie peut être utilisée pour décrire le comportement des étoiles à l'intérieur d'une galaxie et dans ce cas les particules sont des étoiles (typiquement 10 000 000 fois plus massives que la terre!). Dans l'application qui nous intéresse nous pensons plutôt à des molécules et ce cas est évidemment plus simple puisque nous pouvons négliger la contribution de la force de gravité à l'énergie des particules (c.-à-d. le potentiel gravitationnel est essentiellement le même pour toutes les molécules). Dans ce cas, l'énergie d'une particule est dominée par l'énergie cinétique. Comme la géométrie de la molécule est dans un premier temps considérée sphérique, nous nous permettrons de négliger l'énergie de rotation ou de vibration. Nous discuterons plus loin de l'impact de ces processus sur la description microscopique de tels systèmes.

Nous supposons que le volume V contient N molécules ce qui permet de définir la concentration du gaz:

. (1)

Chaque particule est complètement caractérisée par sa position et sa vitesse (direction et grandeur). Toutefois suivant une approche statistique nous pouvons aussi concevoir qu'en considérant l'ensemble des particules nous pouvons définir une vitesse moyenne. Comme cette vitesse est définie dans un espace 3D nous pouvons montrer à partir du théorème de Pythagore que

(2)

Si nous supposons le système isotrope , alors

. (3)

Nous tenterons en premier lieux d'exprimer le concept de pression d'un point de vue microscopique. Supposons qu'une particule se déplaçant sur l'axe des x frappe de façon élastique une surface parallèle au plan y-z (voir figure ci-dessous).

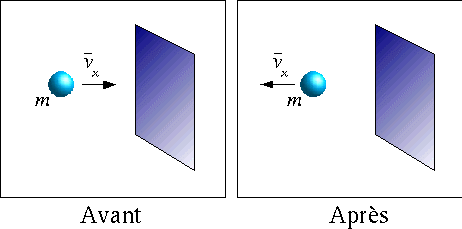
Figure 1: Quantité de mouvement d'une particule avant et après une collision élastique avec une surface perpendiculaire.

Avant la collision la particule possède une quantité de mouvement de alors qu'après la collision la quantité de mouvement de cette même particule devient. Ce qui signifie que la particule a subie une variation de quantité de mouvement . En d'autre terme, la variation de quantité de mouvement par unité de particule est donné par

(4)

Comme la quantité de mouvement doit être conservée, la surface doit absorber exactement la même quantité de mouvement en direction opposée.

Vous avez déjà vu que selon la 2^e loi de Newton,

. (5)

Cette équation peut être exprimée de façon plus générale comme

(6)

En utilisant la notion de différentielle totale et en ne retenant que la composante selon x, nous pouvons écrire:

(7)

Mais le nombre de collision par unité de temps est simplement donné par le produit de la concentration avec le volume formé par le déplacement des particules à la vitesse . Comme les particules doivent faire le trajet aller-retour, il faut toutefois diviser ce nombre par 2.

Figure 2: Volume balayé par un mouvement à vitesse constante pendant un temps infinitésimal dt.

Soitalors nous pouvons déterminer le nombre de collisions par unité de temps comme suit:

(8)

Et donc la force exercée sur la surface A est donnée par

(9)

Par définition la pression est la force par unité de surface

. (10)

En utilisant l'équation 3, nous pouvons réécrire cette équation en fonction de la vitesse quadratique moyenne:

, (11)

que nous pouvons exprimer en fonction de l'énergie cinétique moyenne puisque

(12)

d'où

(13)

Équation que nous pouvons réarranger comme suit

(14)

Pour un gaz parfait, nous pouvons combiner l'équation d'étatavec l'équation 14 afin de mettre en relation la température et l'énergie cinétique moyenne.

soit (15)

Nous pouvons aussi relier la vitesse quadratique moyenne à la température

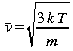(16)

Ce système possède 3 degrés de libertéou 3 paramètres indépendants qui permettent de déterminer son énergie totale (v_x, v_y, v_z). En fait le théorème de l'équipartition de l'énergie propose d'associer une quantité d'énergieà chaque degré de liberté d'un système. Pour un molécule diatomique, nous devons ajouter en principe 3 autres degrés de liberté soit les trois vitesses de rotation perpendiculaires mais si nous prenons en considération que la taille des atomes est très petite devant la distance inter-atomique, nous comprenons que la rotation de la molécule autour de son axe principal contribue de façon négligeable à l'énergie de rotation. Ce système possède donc 5 degrés de liberté actifs. L'énergie moyenne d'une molécule diatomique est donc donnée par

. (17)

Une telle molécule peut aussi entrer en vibration il faut alors ajouter deux autre degrés de liberté puisque nous devons tenir compte de l'énergie cinétique de vibration et de l'énergie potentielle de liaison. Toutefois ces deux degrés de libertés ne deviennent actifs que lorsque . Il s'agit de la limite de cette théorie (voir figure 3). Pour une explication plus élégante de tels systèmes il faut faire appel à la théorie quantique.

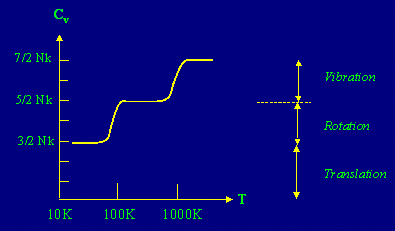
Figure 3: Évolution de la valeur de la chaleur spécifique en fonction de la température pour la molécule H₂. N.B.

Nous avons déterminé la valeur de la vitesse quadratique moyenne mais n'avons pas donné d'information sur la distribution des vitesses ou si vous préférez sur la probabilité de rencontrer une vitesse donnée à l'intérieur du fluide. Maxwell et Boltzmann ont trouvé une réponse à cette question. En particulier, Boltzmann montra que dans un système en équilibre thermique à la température T, la probabilité pour qu'une particule possède une énergie mécanique E est donné par le facteur de Boltzmann

(18)

Pour un gaz parfait, l'énergie est dominée par l'énergie cinétique.

Toutefois plusieurs vecteurs de vitesse différents peuvent conduire à la même valeur d'énergie cinétique (c.-à-d. même norme du vecteur vitesse). On dit alors que le niveau d'énergie est dégénéré. En fait pour bien saisir le concept de dégénérescence, imaginez que l'on forme un espace tridimensionnel qui défini l'ensemble des valeurs possibles de. Les bases de cet espace sont des vecteurs unitaires orientés selon v_x, v_y et v_z. Imaginons que l'on divise cet espace en petits cubes de largeur dv_x , dv_y et dv_z. Chaque cube correspond alors à un état de vitesse unique et possède un volume. Dans cet espace, nous pouvons déterminer le nombre de cubes qui permettent de caractériser un système de vitesse comprise entre v et v+dv. Nous supposons ici que. Dans l'espace des vitesses, cette gamme des vitesses possibles définit une coquille sphérique de largeur dv et de rayon v. Le volume de cette coquille étant donnée par

, (19)

le nombre de cubes contenus dans la coquille est donc proportionnel à, ce qui veut dire que le nombre d'états dégénérés est proportionnel à.

Nous en arrivons à définir la probabilité qu'une particule possède une vitesse comprise entre v et v+dv. Cette probabilité est bien entendu proportionnelle au nombre d'états possibles et donc

. (20)

Comme une particule a 100% de probabilité de posséder une vitesse quelconque,

(21)

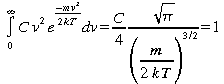(22)

En d'autre termes

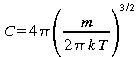. (23)

Ce qui nous conduit à la distribution de Maxwell-Boltzmann

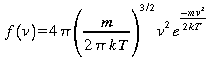. (24)

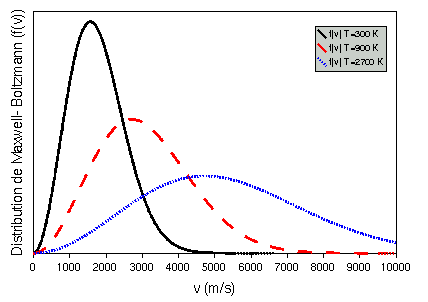
Figure 4: Distributions de Maxwell-Boltzmann pour 3 températures et pour une particule de m=10^-20 kg.