1.4 Calcul de la transmittance totale
La transmittance totale le long d'un parcours![]() est
obtenu par le produit des transmittances liées à la
diffusion par les molécules gazeuses
est
obtenu par le produit des transmittances liées à la
diffusion par les molécules gazeuses
![]() (diffusion de Rayleigh), l'absorption par les molécules
gazeuses
(diffusion de Rayleigh), l'absorption par les molécules
gazeuses
![]() et
l'atténuation par les aérosols
et
l'atténuation par les aérosols
![]() (diffusion
et absorption).
(diffusion
et absorption).
![]() (44)
(44)
Comme le modèle est discret (cases en 3D), il s'avère plus pratique d'exprimer la transmittance totale le long du parcours comme le produit des transmittances de chaque couches individuelles.
![]() (45)
(45)
1.4.1 Diffusion de Rayleigh
Nous supposons que le profil vertical des molécules
stables épouse une décroissance exponentielle avec
l'altitude avec une échelle de hauteur
![]() .
.
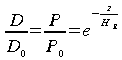 (46)
(46)
Soit la formulation de
![]() donnée
par Kneizys et al. (1980),
donnée
par Kneizys et al. (1980),
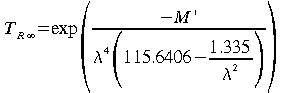 (47)
(47)
![]() où
où
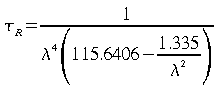 (48)
(48)
où![]() est
la masse d'air corrigée pour la variation de pression au sol
est
la masse d'air corrigée pour la variation de pression au sol![]()
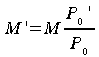 (49)
(49)
Et la masse d'air est donnée par Kasten (1966)
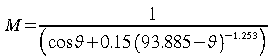 (50)
(50)
Comme la masse d'air est proportionnelle à l'intégrale de la densité du gaz le long du parcours optique et qu'elle est normalisée de telle sorte que la masse d'air totale en visée verticale vaut 1.
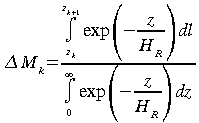 (51)
(51)
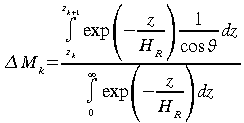 (52)
(52)
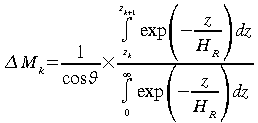 (53)
(53)
pour une visée à travers l'atmosphère
à un angle![]() nous
obtenons donc:
nous
obtenons donc:
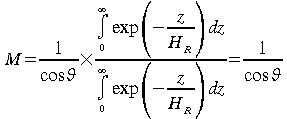 .
(54)
.
(54)
Il s'agit de l'équation approchée de la
masse d'air pour un atmosphère plan parallèle. Pour
corriger la courbure de la terre il faut simplement remplacer le
facteur
![]() par
l'équation 50. Toutefois comme nous voulons appliquer cette
méthodologie à l'échelle urbaine, nous pouvons
faire l'approximation de l'atmosphère plan parallèle.
par
l'équation 50. Toutefois comme nous voulons appliquer cette
méthodologie à l'échelle urbaine, nous pouvons
faire l'approximation de l'atmosphère plan parallèle.
Un problème survient toutefois lorsque![]() car
car
![]() .
Nous corrigerons ce problème en traitant ce cas particulier
en remplaçant l'intégration verticale par une
intégration horizontale.
.
Nous corrigerons ce problème en traitant ce cas particulier
en remplaçant l'intégration verticale par une
intégration horizontale.
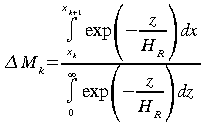 (55)
(55)
soit
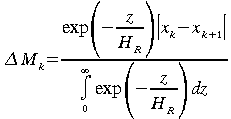 (56)
(56)
Bien entendu ici x2-x1 doit être vu comme la distance horizontale entre les deux points (nous travaillons en 3D!).
Comme
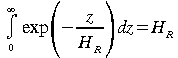 (57) et
(57) et
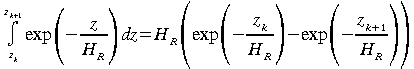 ,
(58)
,
(58)
Nous pouvons exprimer les équations 53 et 56 de la façon suivante:
![]() :
:
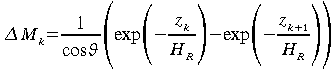 (59)
(59)
![]() :
:
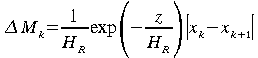 (60)
(60)
Nous pouvons donc exprimer la transmittance du parcours optique k comme:
![]() (61)
(61)
où l'élément de masse d'air corrigé pour les variations de pression atmosphérique au sol est donné par:
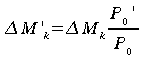 (62)
(62)
1.4.2 Absorption par les gaz
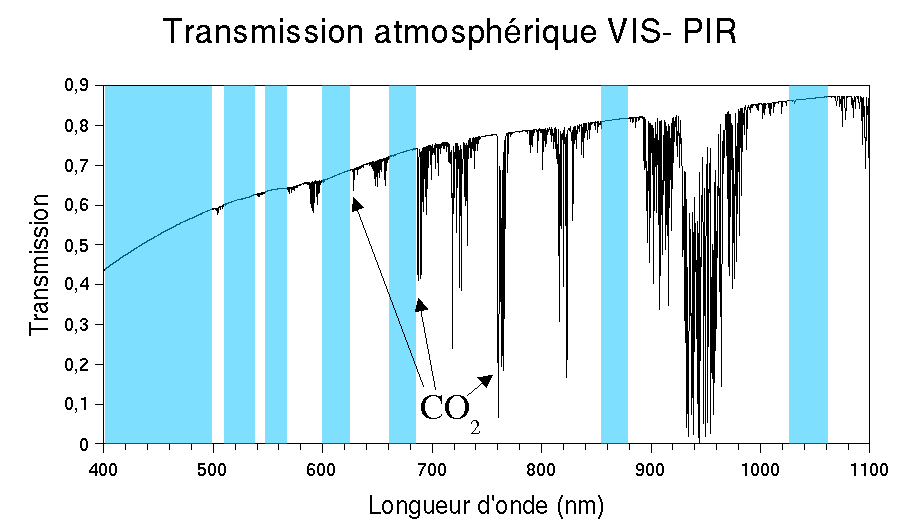
Se référer au document EXCEL sur la page du cours pour estimer l'absorption par bandes spectrales (bandes de votre choix) en se concentrant principalement sur le CO2 et H2O. Sur la courbe ci-dessous, les variations de très hautes fréquences sont dues au phénomène d'absorption alors que la dépendance lente est due à la diffusion de Rayleigh. Vous pouvez pondérer la transmittance moyenne par bandes spectrales en proportion de la masse d'air considérée pour une couche atmosphérique k de la façon suivante:
![]()
![]() est
la transmittance moyenne de la bande donnée par les courbes
d'absorption du CO2 et H2O, elle correspond à
la portion de la transmittance provenant de l'absorption de ces deux
gaz sur toute l'atmosphère en visée verticale.
est
la transmittance moyenne de la bande donnée par les courbes
d'absorption du CO2 et H2O, elle correspond à
la portion de la transmittance provenant de l'absorption de ces deux
gaz sur toute l'atmosphère en visée verticale.
1.4.3 Atténuation par le aérosols
Par définition, la transmittance des aérosols est donnée par,
![]() .
(63)
.
(63)
Si l'atmosphère est subdivisée en
superposition de couches discrètes d'incrément
d'épaisseur optique![]() nous
pouvons exprimer l'équation ci-dessus comme suit:
nous
pouvons exprimer l'équation ci-dessus comme suit:
![]() .
(64)
.
(64)
Si nous supposons que le profil vertical des aérosols
est exponentiel avec une échelle de hauteur
![]()
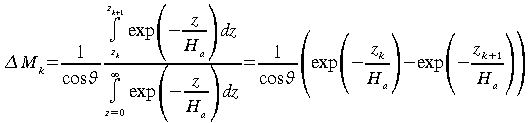 (65)
(65)
De façon analogue aux équations 53 et 56 nous pouvons écrire:
![]() :
:
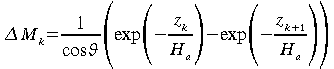 (66)
(66)
![]() :
:
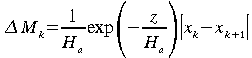 (67)
(67)
Je vous suggère de vous référer à des climatologies de l'épaisseur optique des aérosols pour déterminer ce paramètre. Une bonne référence serait le Global Aerosol Data Set (GADS).
Références
Kasten, F., "A New Table and Approximate Formula for Relative Optical Air Mass," Arch. Meteorol. Geophys. Biochlimatol., Ser. B14, 1966, pp. 206-223.
Kneizys, F. X., E. P. Shettle, W. O. Gallery, J. H. Chetwynd, Jr., L. W. Abrea, J. E. A. Selby, R. W. Fenn, and R. W. McClatchey, Atmospheric Transmittance/Radiance: Computer Code LOWTRAN5, Tech. Rep. AFGL-TR-800067, Bedford, MA: U.5. Air Force Geophysics Laboratory, 1980.