Chapitre 5: Interaction électromagnétique

5.1 Les équations de conservation sous forme différentielle

La conservation de l'énergie s'exprime comme suit:

En fait cette équation énonce que si un système est isolé, son énergie totale est constante seule les formes d'énergies peuvent changer. En d'autres termes,

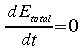
Supposons que l'énergie dépende de plusieurs variables comme par exemple E=f(u, v, w,...) et que chacune de ces variables dépend à son tour du temps, nous pouvons utiliser la différentielle totale pour décrire la variation temporelle de l'énergie.

représente la dérivée partielle de l'énergie par rapport à la variable u. Cette dérivée est évaluée en considérant que toutes les autres variables en jeu comme des constantes à l'exception bien entendu de u.

Pour un système donné, nous devons dans un premier temps construire la forme le plus générale de l'énergie totale. Par exemple supposons un système ayant une masse m et un volume V qui est à une certaine température T et qui possède une chaleur spécifique volumique C_v. Nous supposons de plus que ce système peut transférer son énergie sous forme radiative. L'émissivité de la masse est e, et sa surface totale A. Pour simplifier nous admettons que ce système est disposé dans une espace maintenu à 0 Kelvin.

L'énergie est accumulée sous forme thermique dans la masse et si la température du corps est diminuée, l'énergie accumulée sera réduite.

(énergie thermique interne)

L'énergie perdue par unité de temps sous forme radiative est donnée par

(corps noir)

Ainsi l'équation de conservation d'énergie dans ce cas particulier peut s'écrire:

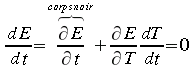
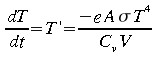(5.1)

5.2 Résolution d'équations différentielles

Solution analytique: Pour certaines équations différentielles particulièrement simples, il est possible de se rattacher à une solution analytique. Cette situation est plutôt rare lorsqu'on étudie des systèmes naturels. L'équation 5.1 répond toutefois à cette condition. L'équation 5.1 peut être réarrangée de la façon suivante qui consiste à regrouper les variables de même nature de part et d'autre de l'égalité.

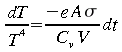
En prenant l'intégrale de part et d'autre de l'égalité, nous obtenons:

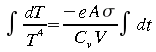
ce qui conduit à la solution analytique suivante:

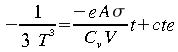
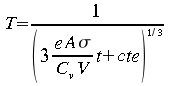
À t=0, cette équation se résume à 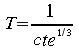d'où

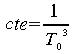
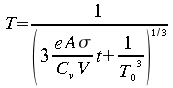
Exemple: Nous prendrons pour acquis que e=1, A=6 m², C_v=4,19x10⁶ J/m³/K, V=1 m³ et J/m²/K⁴. Soit T₀=1000 K à t=0 et posons pour alléger l'écriture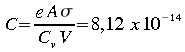

À t=10000 s, la solution analytique donne T=662,67 K.

Dans la prochaine section nous comparerons ce résultat avec différentes méthodes de résolution numérique.

5.3 Méthodes d'intégration numérique

La solution analytique de la majorité des équations différentielles n'est pas connue. Avec l'augmentation fulgurante de la puissance de calcul des ordinateurs (double à tous les 18 mois) des méthodes de résolution numérique ont été développées. Dans cette section, nous en passerons en revue quelques unes. Ce document ne se veut pas être une revue complète de ce domaine mais doit être vu comme un document d'initiation. Vous devriez y retrouver les éléments le plus importants qui vous permettrons de résoudre la plupart des équations différentielles que vous rencontrerez durant ce cours.

• Méthode de Euler

La méthode de Euler est sans doute le plus simple de toutes. Elle a l'avantage d'être facile à implémenter mais elle génère d'importantes erreurs numériques.

¹

L'erreur de cette méthode est proportionnelle à. Toutefois comme le nombre de pas de calcul varie enoù T est la durée totale de la modélisation, l'erreur totale cumulée est donc proportionnelle à.

• Méthode de Verlet (ordre 2)

• Runge-Kutta (ordre 4)

Posons

où

Cette méthode peut être généralisée au cas de plusieurs variables en ajoutant simplement pour chaque nouvelle variable une fonction du type

avec

• Développement en série de Taylor

Prenons l'expansion de Taylor de la fonction x par rapport à la variable t et en conservant les cinq premiers termes

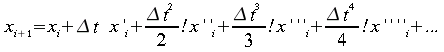
En appliquant à nouveau ce type de développement pour et(doit être remplacé respectivement paret), on trouve (après quelques manipulations algébriques) la formule d'Adam d'ordre 4 ci-dessous:

Les deux premier de cette formule correspondent exactement à la méthode de Euler présentée précédemment. En d'autres termes, la méthode de Euler correspond à la formule d'Adam d'ordre 1.

Les 3 premiers termes correspondent quant à eux à la méthode de Verlet si on suppose que

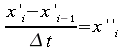
La méthode de Verlet correspond donc à la formule d'Adam d'ordre 2.

En regroupant les termes semblables, la formule d'Adam d'ordre 3 peut s'écrire comme suit:

(formule d'Adam d'ordre 3)

Une des versions les plus utilisées de cette méthode est la formule d'ordre 4 qui s'écrit comme suit:

(formule d'Adam d'ordre 4)

Cette dernière méthode nécessite 5 conditions initiales soient. La méthode de Runge-Kutta peut être employée pour générer les données initiales manquantes.

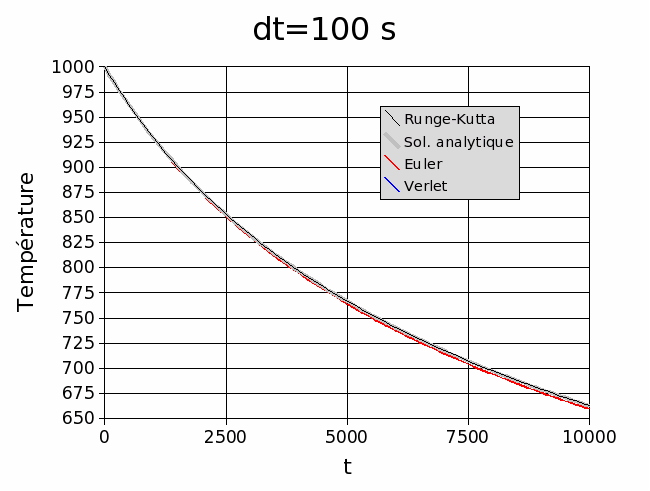
Exemple: Nous allons trouver la solution numérique de l'équation 5.1 en posant un pas de calcul de 1000 sec.

La solution analytique donne T₁=929,85 K (pour t=1000s)

Solution avec Euler:

Solution avec Verlet:

Solution numérique avec Runge-Kutta,

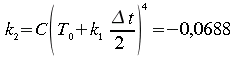
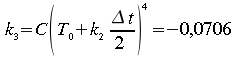
La méthode de Runge-Kutta génère donc seulement 0,006% d'erreur même pour un pas de calcul aussi grand que 1000 secondes.

Comparaison des trois méthodes de résolution pour deux pas de calcul: 1000 s et 100 s

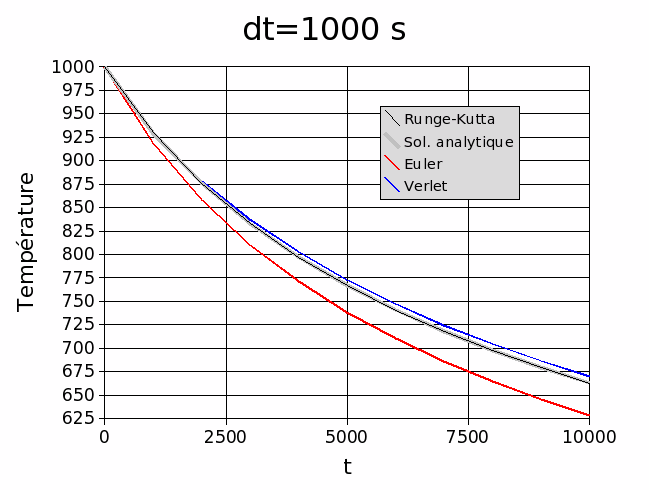
Nous pouvons complexifier davantage le problème en ajoutant un transfert énergétique sous forme de conduction thermique. Si la masse repose dans l'air dont la conductivité thermiqueet si nous omettons de considérer la convection (i.e. pas de gravité), on peut montrer que pour écrire l'équation de conservation de l'énergie, nous devons ajouter le terme

x représente la direction perpendiculaire au flux d'énergie de sorte que représente le gradient de température. En réalité le gradient s'exprime de la façon suivante en 3 dimensions

Le gradient est une quantité vectorielle qui indique toujours la direction de changement maximal de la variable considérée en fonction de la position.

En une dimension la conservation de l'énergie prend la forme suivante.

Comme cette équation fais maintenant intervenir une dérivée spatiale, nous devrons la résoudre pour chaque élément de l'espace (cellule) de façon indépendante en considérant dans un premier temps le gradient de température à t=0 dans le voisinage immédiat de la cellule comme étant constant dans le temps. Après avoir résolu numériquement l'équation ci-haut pour le temps , nous reprenons le calcul en déterminant les nouveaux gradients donnés par les nouvelles températures, et ainsi de suite.

La valeur approchée du gradient peut être déterminée comme suit:

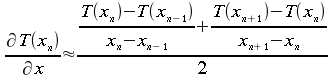
5.4 Angle solide

L'angle solide représente le rapport de la surface d'un objet projetée sur une sphère ayant un rayon égal à la distance objet-observateur sur le carré de la distance objet-observateur.

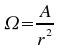(str)

L'angle solide correspondant à toutes les directions est égal à . Les « unités » de l'angle solide sont notées stéradians (str). En réalité il ne s'agit pas d'une unité à strictement parler puisque l'angle solide est adimentionnel.

Si l'objet considéré est petit devant la distance r, nous pouvons écrire:

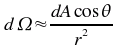
où l'angle est mesuré entre la normale à la surface dA et la ligne de visé.

5.5 Intensité lumineuse

Nous définissons d'abord la puissance émise, transportée ou reçue par un objet (en W) comme le flux énergétique (). Dans le cas particulier d'une source lumineuse, le flux énergétique représente la puissance lumineuse émise dans toutes les directions. Si nous sommes intéressés à connaître la puissance émise dans une direction particulière, il devient nécessaire de définir une puissance par unité d'angle solide.

(W/str)

Cette quantité est précisément l'intensité énergétique (ou lumineuse). Pour une source ponctuelle isotrope, l'intensité lumineuse est simplement donnée par

Si vous connaissez l'intensité d'une source dans une direction donnée et que vous voulez savoir combien de watts traverserons une surface dA, vous n'avez qu'à calculer le produit:

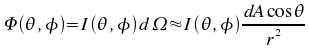
5.6 Luminance

La luminance (L) est l'intensité lumineuse provenant d'une source étendue mesurée par unité de surface apparente de la source. Si la surface émettrice n'est pas perpendiculaire à la direction d'émission de la lumière alors il faut faire une projection en .

5.7 Irradiance

L'irradiance, ou exitance énergétique (M), est le flux émis par une source dans toutes les directions par unité de surface émettrice. C'est ce concept qui intervient dans loi de Stephan qui permet de calculer l'irradiance d'un corps noir en fonction de sa température.

5.8 Éclairement

L'éclairement (E) est une grandeur liée à une surface réceptrice de rayonnement. L'éclairement représente le flux reçu par unité de surface. Nous avons déjà discuté de ce concept sans le nommer lorsque nous parlions de la constante solaire.

Il est important de mentionner que les quatre dernières définitions peuvent être aussi définies par unité de longueur d'onde en prenant en considération la dépendance de la grandeur considérée en fonction de la longueur d'onde de la lumière. Nous parlerons alors, d'intensité spectrale, éclairement spectral, etc.

Par exemple: Irradiance spectrale

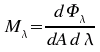
De plus,

5.9 Induction électromagnétique

Un charge mobile soumise à un champ électrique oscillant de manière sinusoïdal est entraînée par ce dernier dans un mouvement sinusoïdal. En effet comme l'onde électromagnétique est composée en particulier d'un champ électrique et que le champ électrique est défini comme la force par unité de charge, la charge sera soumise à un force d'entraînement de la forme:

q étant la charge mobile.

Comme nous pouvons écrire

En réorganisant cette équation nous trouvons

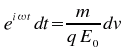
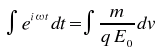
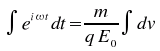
d'où

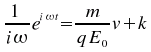
soit

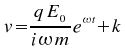si on pose la vitesse moyenne nulle, alors k=0

Nous prenons la partie réelle de cette équation (n.b. Ceci implique que nous avons supposé que la force est une fonction ).

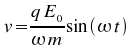
Comme la position de la charge est donnée par l'intégrale de la vitesse, nous trouvons

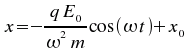
Autrement dit, une particule soumise à un champs électromagnétique sinusoïdal se déplacera selon un mouvement sinusoïdal de même fréquence mais avec une amplitude inversement proportionnelle au carré de la fréquence de inversement proportionnel à sa masse. Nous pouvons remarquer que l'amplitude du mouvement sera aussi proportionnel à la charge. Les charges mobiles les plus courantes sont bien entendu les électrons. Nous ne considérerons donc pas la dépendance en m et q dans ce cours.

5.10 Rayonnement de Bremsstrahlung

Une charge qui est accélérée avec une accélération a (vitesses faibles) émet de la radiation électromagnétique selon l'équation d'intensité suivante:

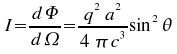(W/str)

Cette fonction montre une valeur maximale pour les directions perpendiculaires à la direction de l'accélération et est nulle dans la direction de l'accélération. Le rayonnement de Bremsstrahlung fait perdre de l'énergie à toute charge accélérée (comment concilier cela avec les orbitales atomiques???).

5.11 Rayonnement d'un dipôle

Sauter cette section!

5.12 Propriétés diélectriques des matériaux

Un milieu diélectrique est un milieu faiblement conducteur mais qui a la propriété de favoriser le « transport » du champ électrique.

Vous avez probablement déjà vu que le champ électrique produit par une charge est inversement proportionnelle à la permittivité du vide .

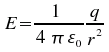(loi de Coulomb)

Cette loi peut être généralisée à un milieu diélectrique quelconque simplement en remplaçant par , ou est la constante diélectrique du matériau.

La constante diélectrique représente la capacité des dipôles électriques contenus dans le matériaux à s'aligner dans la direction du champ électrique. Si l'alignement est grand, alors le champs électrique peut être inférieur à l'intérieur du matériau ().

5.13 Indice de réfraction

La constante diélectrique qui dépend de la fréquence du rayonnement électromagnétique considéré, est lié à l'indice de réfraction de la façon suivante:

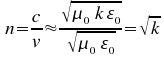car

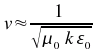
Pour être plus général on exprime généralement l'indice de réfraction sous une forme complexe

n_r est l'indice de réfraction réel qui permet d'expliquer la déviation de la lumière alors que n_i permet de prendre en considération l'absorption de la radiation par une matériau.

5.14 Réflexion

Il y a réflexion lorsque la radiation incidente sur une surface est retournée en direction inverse sans changer de fréquence. Nous pouvons comprendre ce processus en admettant que le champ électrique atteignant la surface fait osciller les charges libre de la surface et ces dernières étant accélérées émettent cette radiation en théorie dans toutes les directions mais comme la lumière ne traverse pas la surface, la seule direction possible est la direction inverse à la direction d'incidence. La réflexion peut être soit spéculaire ou diffuse. Lorsque la réflexion est spéculaire, l'angle d'incidence est identique à l'angle de réflexion en référence à la normale de la surface réfléchissante. Dans le cas de la réflexion diffuse, la radiation part dans plusieurs directions après avoir atteint la surface. Il est possible d'expliquer la réflexion diffuse si nous considérons la surface diffusante comme une surface irrégulière soit une collection d'une multitude de surfaces ayant une certaine distribution de la direction de la normale.

5.15 Réflectance

La réflectance est la fraction de l'énergie réfléchie sur la fraction incidente. Cette fraction est propre à un matériau donné mais pour un même matériau elle dépend de la fréquence de la lumière.

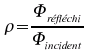
5.16 Réflectance bi-directionnelle

Comme la réflectance peut varier avec l'angle d'incidence et l'angle de réflexion (réflexion diffuse), il est pratique de définir le facteur de réflectance bi-directionnelle (BRDF). La BRDF est une fonction des angles d'incidence et de réflexion. Elle permet de convertir une puissance incidente en puissance réfléchie par unité d'angle solide et par unité de surface apparente en fonction de la géométrie d'éclairement et d'observation.

(1/str)

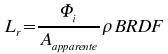
Un cas particulier simple et idéalisé de la BRDF est le cas de la réflectance Lambertienne. Dans ce cas, on suppose que la luminance est redistribuée également peu importe la valeur des angles d'incidence et de réflexion.

Le facteur est introduit puisque toutes les directions de réflexions possible totalisent un angle solide de (un hémisphère) .

Ainsi nous pouvons dans ce cas écrire:

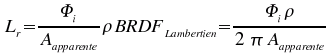
Le cas Lambertien est souvent utilisé en modélisation en raison de son agréable simplicité. Certains modèles un peu plus sophistiqués ajoutent un terme correctif pour tenir compte d'une fraction réfléchie de manière quasi-spéculaire. Toutefois il est sûrement avantageux de faire des mesures ou de la modélisation dans des conditions le plus éloigné possible de l'angle de réflexion spéculaire.

Parenthèse: Le « hot spot » en télédétection vs couvert végétal.

5.17 Transmittance

La transmittance représente la fraction du flux incident sur un volume de matériau translucide qui réussit à le traverser. Comme le flux total doit être conservé, nous pouvons exprimer le principe de conservation de l'énergie comme suit.

Où R représente la fraction de la radiation qui a changée de direction suite à une interaction avec des éléments de matière contenue dans le volume. Il s'agit en quelque sorte d'une forme de coefficient de réflexion qui peut être tout à fait comparé au concept de réflectance d'une surface mais qui est appliqué au cas d'un volume. On parle d'ailleurs fréquemment de réflectance atmosphérique par exemple dans le domaine de l'optique atmosphérique. Le coefficient du troisième terme de cette équation de conservation (A) représente la fraction du flux incident qui a été absorbée dans le parcours. La diffusion consiste en un changement de direction de la radiation incidente sans modification de la fréquence de la radiation. Il s'agit en quelque sorte d'une réflexion du photon sur la particule de matière. Lorsqu'il y a absorption, l'énergie du photon est entière convertie en énergie thermique. Cette énergie sera éventuellement ré-émise sous forme radiative selon la loi de Planck.

La transmittance totale le long d'un parcourspeut aussi être exprimée comme le produit des transmittances liées à la diffusion et à l'absorption. Prenons le cas de l'atmosphère, la transmittance totale est causée par la diffusion des molécules gazeuses(diffusion de Rayleigh), l'absorption par les molécules gazeuseset l'atténuation par les aérosols(diffusion et absorption). Les aérosols sont des particules de la taille du micron.

(44)

De plus si nous considérons le volume d'air comme une superposition de couches atmosphériques, il peut s'avérer utile d'exprimer la transmittance totale le long du parcours comme le produit des transmittances de chaque couche individuelle.

(45)

5.19 Épaisseur optique et le coefficient d'Ångström

L'intensité d'un faisceau qui traverse un milieu absorbant et diffusant est diminuée en raison de l'atténuation par un facteur _, où est défini comme étant l'épaisseur optique d'atténuation (AOD). Vous aurez sans doute compris que l'AOD est intimement liée au concept de transmittance totale introduit précédemment.

L'AOD est le résultat de l'atténuation totale sur toute la colonne atmosphérique. Il peut être exprimé en fonction du coefficient d'atténuation .

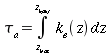(3)

Le coefficient d'atténuation, qui possède des unités de m^-1, dépend de la section efficace d'atténuation pondérée par la concentration en particules. La section efficace représente la surface effective d'interaction couverte par une particule de telle sorte que le rapport de cette surface sur une surface de référence de 1 m² soit égale à la probabilité d'interaction entre la radiation lumineuse et la particule. La section efficace est intimement liée à la taille de la particule par le biais de l'efficacité d'atténuation . L'efficacité d'atténuation est en effet définie comme le rapport de la section efficace d'atténuation sur la section géométrique de la particule.

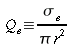(4)

Le coefficient d'atténuation peut être exprimé comme l'intégration sur la taille des particules de la section efficace multipliée par la concentration par unité de taille de particule [unités de particules . m^-4], étant le nombre de particules par unité de volume [particules . m^-3].

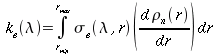(5)

Si nous observons une source lumineuse à travers un milieu translucide, et que la lumière de la source est plus intense que la lumière diffuse ambiante, les deux phénomènes (absorption et diffusion) conduisent à une réduction de l'intensité de la lumière sortante ou atténuation.

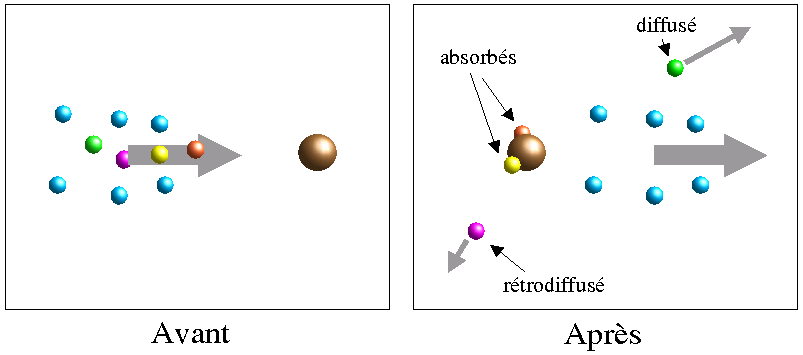
Figure 5: Origine de l'atténuation de la radiation. Les petites sphères correspondent au photons alors que les grandes sphères marrons représentent les aérosols.

La section efficace d'atténuation est simplement la somme de la section efficace de diffusion et de la section efficace d'absorption.

(6)

Petite démonstration 1: Probabilité de collision (dP) dans un élément de volume

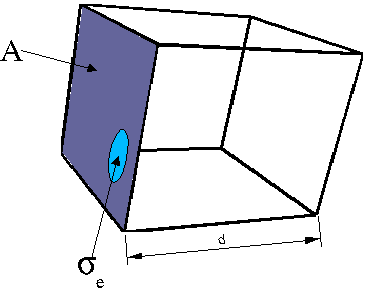
Figure 6: Géométrie du problème de l'atténuation

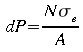(7)

N est le nombre de particules dans l'élément de volume considéré, A est la surface de l'élément de volume normale au flux incident.

(8)

(9)

(10)

Petite démonstration 2: Atténuation exponentielle pour le cas où la concentration et le type de particule ne dépend pas de la position (c.-à-d. est constant).

(11)

(12)

(13)

(14)

(15)

(16)

(17)

Nous définissons , mais cette équivalence n'est valide que si est indépendant de la position.

La section efficace et par conséquent est dépendante de la longueur d'onde. Dans le spectre visible, varie en où , le coefficient d'Ångström, avoisine l'unité pour une distribution de taille log-normale centrée sur une taille moyenne de quelques centièmes de microns. En d'autres termes, dans ce cas, varie en (diffusion de Mie, Van de Hulst (1957)). Plus la taille des particules est petite, plus est grand. Une valeur limite supérieure est toutefois atteinte lorsque alors que la limite inférieure est 0. La limite supérieure correspond au comportement spectral de l'épaisseur optique d'atténuation associée aux particules beaucoup plus petites que la longueur d'onde telles que les molécules gazeuses de l'atmosphère (diffusion de Rayleigh). La limite inférieure correspond au cas où la taille des particules est hautement supérieure à la longueur d'onde. Les micro-gouttelettes d'eau contenues dans les nuages correspondent à cette condition, ce qui explique la couleur blanche des nuages. En effet, dans ce cas, toutes les longueurs d'ondes visibles sont essentiellement diffusées de la même façon.

Le comportement spectral de l'AOD peut donc être décrit à l'aide du coefficient d'Ångström par l'équation 18.

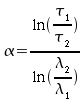ou (18)

Ici, et sont respectivement les mesures de l'épaisseur optique réalisées aux longueurs d'ondes et . Le coefficient d'Ångström, comme l'épaisseur optique à deux longueurs d'ondes, peut donc être considéré comme un indicateur de la taille moyenne de la distribution de taille des aérosols. Généralement lorsque est grand, la distribution de taille est petite et inversement. Toutefois, lorsque la distribution de taille des particules est étroite (gamme restreinte de tailles), il se peut que le comportement spectral s'éloigne significativement de l'équation 18 car cette situation favorise le phénomène d'interférence (constructive ou destructive) entre la lumière diffractée par la particule et la lumière transmise à travers la particule. Ce phénomène se produit lorsque le retard de phase entre les deux rayonnements est un multiple de . La figure 7 illustre le phénomène pour une modélisation du cas des sphères non-absorbantes. Le comportement spectral oscillatoire de l'efficacité d'atténuation apparaît lorsque le diamètre des particules est supérieur ou égal à la longueur d'onde .

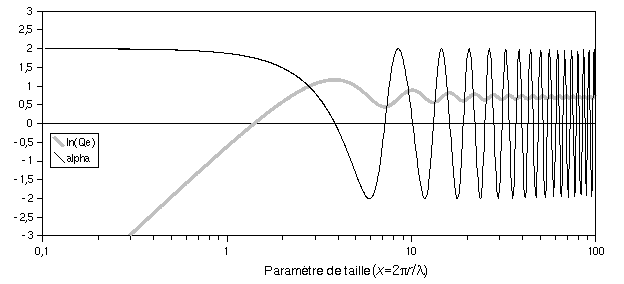
Figure 7: Comportement spectral de l'efficacité d'atténuation et du coefficient d'Ångström (alpha) pour une sphère non absorbante selon Van de Hulst (1957), section 11.22.

5.20 Masse d'air

Le concept de masse d'air est très utile car il permet de passer d'une expression de l'épaisseur optique d'un volume et concentration témoin dans une direction normale à un changement de direction ou de concentration. Ce concept a été d'abord introduit en astrophysique pour permettre la correction des images acquises par les télescope en fonction de l'angle de visé par rapport au zénith (point le plus haut dans le ciel). En effet si nous connaissons l'épaisseur optique pour un angle zénithal, nous pouvons connaître l'épaisseur optique pour un angle de visé quelconque. Bien entendu nous devons dans ce cas supposer une isotropie de la distribution des composants atmosphériques.

Un exemple avec la diffusion de Rayleigh de l'atmosphère terrestre:

Nous supposons que le profil vertical des molécules à concentrations stables de l'atmosphère terrestre épouse une décroissance exponentielle avec l'altitude avec une échelle de hauteur .

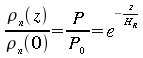(46)

Soit la formulation empirique dedonnée par Kneizys et al. (1980),

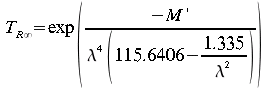(47)

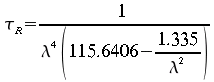où (48)

oùest la masse d'air corrigée pour la variation de pression au sol

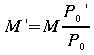(49)

Et la masse d'air est donnée par Kasten (1966)

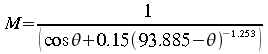(50)

La masse d'air est proportionnelle à l'intégrale de la densité du gaz le long du parcours optique et qu'elle est normalisée de telle sorte que la masse d'air totale en visée verticale vaut 1.

L'équation approchée de la masse d'air pour un atmosphère plan parallèle est donnée par:

. (54)

L'équation 50 permet donc de corriger pour l'effet de la courbure de la terre.

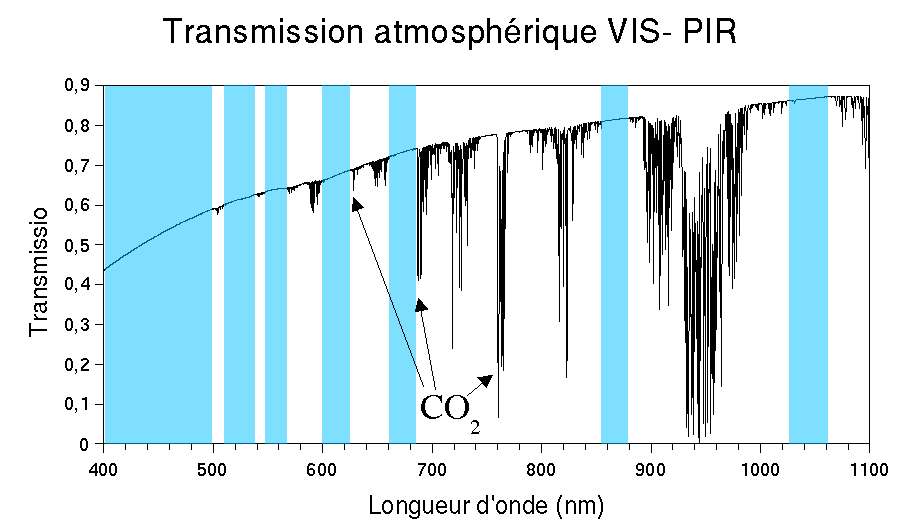
Transmittance atmosphérique dans le domaine visible et proche infrarouge.

Les zones ombragées sur la figure ci-dessus son couramment appelés fenêtres atmosphériques. Dans ces zones, l'absorption moléculaire des molécules à concentrations hautement variables (H₂O, CO₂). Dans les fenêtres atmosphériques, l'atténuation est moins grande et surtout plus facile à modéliser. Ce sont donc des longueurs d'ondes privilégiées en télédétection et en astrophysique.