Chapitre 3: Physique des ondes

3.1 Définition et nature d'une onde

• déformation qui se propage dans un environnement

• Ex.

• modèle microscopique de la matière

• réseau d'atomes

• propriétés d'une onde et de son milieu (amplitude, vitesse)

3.2 Types d'ondes

• Longitudinales

• transversales

3.3 Le principe de superposition

3.4 Oscillateur harmonique

• Système masse ressort

  

posons

d'où

3.5 Ondes sinusoïdales

,

T= période [s], f=fréquence [s^-1 = Hz], k=nombre d'onde, = longueur d'onde

Une relation très importante entre la vitesse, la fréquence et la longueur d'onde:

3.6 Notation de Euler

Nombre imaginaire i

,

faisons de développement en série de Taylor de autour de x=0.

et donc

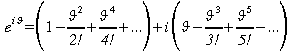
La parenthèse de gauche est le développement de Taylor dealors que la parenthèse de droite est le développement de!

(formule de Euler)

la partie réelle correspond à un cosinus alors que la partie imaginairecorrespond à un sinus.

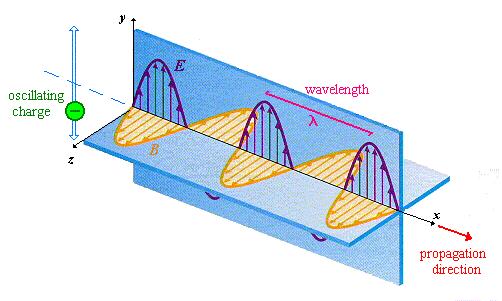
3.7 Onde électromagnétique

Intensité lumineuse:

(onde plane)

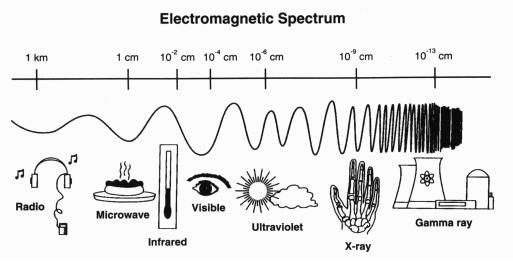
3.8 Spectre électromagnétique

3.9 Résonance, harmoniques, ondes stationnaires, et facteur de qualité

Soit deux ondes identiques qui se rencontrent en sens opposés,

Ce résultat indique que la forme de l'onde résultante est fixe mais son amplitude varie dans le temps. Il s'agit d'une onde dite stationnaire. Si de telles ondes se retrouvent dans un endroit de dimension limitée alors nous voyons apparaître le phénomène de résonnance. Lorsqu'il y a résonnance, certaines longueurs d'ondes sont favorisées au détriment de autres. Ce sont les conditions frontières qui déterminent cette sélection de longueurs d'ondes. L'exemple de la corde de guitare est un des plus simple à visualiser. Dans ce cas, les points d'attache de la corde ne peuvent pas bouger et il faut donc imposer qu'à ces endroits, l'amplitude de l'onde stationnaire est toujours nulle. On nomme les points d'amplitude nulle le noeuds alors que les maximums d'amplitude sont les ventres.

Exercice 1:

À partir de l'équation du champ électrique total pour l'onde stationnaire, exprimez l'équation d'onde de la corde de guitare de 75 cm de longueur. Dans ce cas, le champ représente la hauteur de la corde.

a) Pouvez vous dériver cette équation pour déterminer la position des maximums et minimums.

b) En supposant qu'il y a seulement des noeuds aux points d'attaches et que la fréquence de l'onde émise est le la 440 Hz, déterminez la vitesse de l'onde dans le corde. Réponse: 660 m/s

c) Un musicien expérimenté arrive à faire émettre une onde de 880 Hz à cette même corde. Si la vitesse des ondes est constante, comment peut-il réussir à émettre un tel son.

Indice: Considérez qu'il puisse y avoir plus de deux noeuds.

d) Pouvez vous expliquer par analogie l'effet amplificateur d'une antenne pour les ondes électromagnétiques?

e) Calculez la longueur de la tige de métal qui ferait l'antenne idéale pour émettre la fréquence FM de 101.1 MHz. Réponse: 5,93 m

3.10 Série de Fourier

Toute fonction périodique peut-être décomposée par une somme discrète de sinus et cosinus.

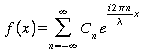
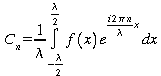
ex.: Onde carrée

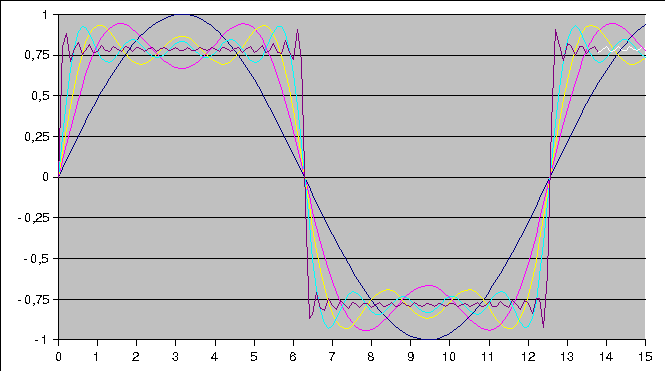
(a)

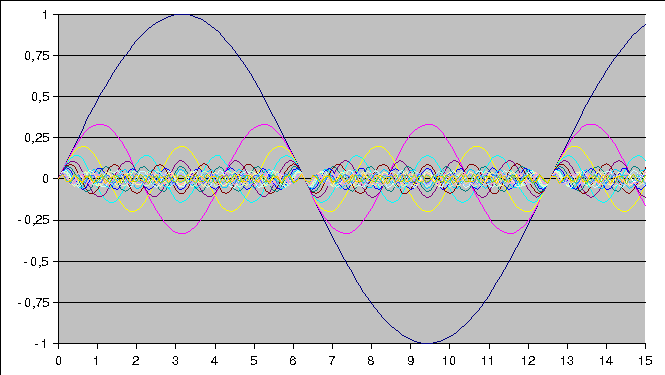
(b)

Reconstitution (a) et décomposition d'une onde carrée à l'aide du 1er, des 3 premier, des 5 premiers puis des 20 premiers termes de la série de Fourier.

Exercice 1:

Soit la fonction ,

a) Calculez les C_n de cette fonction.

réponse: C₀=A/2, C₁=C_-1=-A/4, tous les autres C_n sont nuls

b) À partir des valeurs de C_n, écrivez la fonction f(x) sous forme de série de

Fourier.

réponse:

c) Entrez cette série dans excel et tracez la fonction en posant k=2 et A=1.

d) Vous venez de démontrer (en b) une identité trigonométrique. Laquelle?

Exercice 2:

Trouvez les C_n de la fonction , où M et A sont des constantes.

Exercice 3:

Soit la fonction périodique en dent de scie qui est donnée par la fonction et dont le cycle mesure 1 m, trouvez les 5 premières valeurs de C_n (c.-à-d. n compris entre -2 et 2). Tracez la somme de ces 5 premiers termes sur un chiffrier et comparez les à la fonction initiale. Commentez.

Exemple 1: L'interférométrie pour repousser la limite instrumentale occasionnée par le diffraction.

Dans le sud de la France, vers la fin des années 80, un astronome Français A. Labeyrie à mis au point un système composé de deux télescopes de 1.5 m de diamètre dont les faisceau optiques sont combinés (interférence) dans un laboratoire situé entre les deux instruments. Ce système peut être apparenté aux fentes de Young avec la différence que la distance séparant les deux télescopes peut être modifiée à volonté. Si les deux télescopes pointent la même étoile, et qu'on les déplace, cela a pour effet de modifier la distance séparant les « fentes ». L'équation ci-dessous décrit la dépendance de l'intensité lumineuse en fonction de la distance entre les télescopes x.

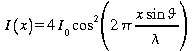où est l'angle entre la perpendiculaire à la ligne reliant les deux télescopes avec la direction de visée.

Supposez que deux étoiles sont présentes dans le champ à des angles suffisamment rapprochés pour qu'elles ne puissent pas être séparées par un télescope traditionnel et supposez que les intensités sont additives (les deux sources ne sont pas cohérentes), on s'attend à obtenir un signal de la forme donnée par la courbe noire ci-dessous. L'analyse de cette courbe avec la série de Fourier permet de réaliser que cette courbe est décomposable en un C₀ constant (sans intérêt ici) et deux fonction cosinus

et (courbes grise et pointillée ci-dessous)

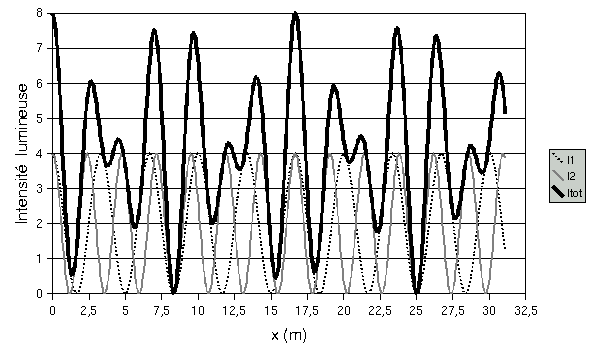
Mais si nous faisons l'hypothèse que la seconde équation provient de l'image d'une étoile légèrement décalée d'un angle par rapport à la première, si nous utilisons le résultat de l'exercice précédent sur l'analyse de Fourier de la fonction et si nous considérons que ce système se comporte comme les fentes de Young, nous pouvons en déduire que

et ,

et donc déterminer la valeur de (k₁ et k₂ correspondent aux nombres d'ondes des C_n non nuls).

En d'autre termes, l'analyse de Fourier a permis de mesurer l'angle séparant deux étoiles même si chaque appareil utilisé ne permet pas de le discriminer. En généralisant cette méthode, l'équipe de A. Labeyrie a réussi à mesurer le premier diamètre d'étoile (autre que le soleil).

3.11 Transformée de Fourier

Si nous admettons que la fonction puisse avoir une période infinie, nous pouvons généraliser la série de Fourier au cas continu en prenant la limite.

(transformée de Fourier inverse de)

=nombre d'onde

(transformée de Fourier de )

représente le spectre de fréquences spatiales de .

Exercice:

Utilisez un algorithme de transformée de Fourier rapide (FFT) pour traiter un certain nombre de forme simples. Inversez le processus pour vérifier si vous retombez sur la fonction initiale. Un algorithme FFT est disponible gratuitement sur le www.fftw.org (FFTW, fastest fourier transform in the west). Cet algorithme est entre autre intégré au progiciel octave (un équivalent linux de matlab) ce qui facilite son utilisation. Vous pourrez même aller jusqu'à tester la convolution et déconvolution qui seront introduites ci-dessous. Je vous invite à explorer aussi les capacités de matlab en cette matière.

3.12 Opérations dans l'espace de Fourier

Convolution de deux fonctions:

Imaginez que vous voulez lisser une fonction avec une courbe gaussienne de la forme:

.

La méthode classique pour procéder à cette opération consiste à faire glisser la fonctionsur la fonctionen les multipliant point à point et en sommant l'ensemble de ces produits. Il pourrait alors être avantageux de passer dans l'espace de Fourier. En effet si vous prenez la transformée de Fourier de, la transformée de Fourier deet que vous en prenez le produit, pour enfin prendre la transformée de Fourier inverse de ce produit, vous venez de faire la convolution deet .

Déconvolution de deux fonctions:

L'opération inverse peut aussi être réalisée. Il s'agit de prendre le rapport des transformées de Fourier.

Cette opération peut par exemple servir à augmenter la résolution d'un spectre ou d'une image si on connaît la fonction qui représente le plus fin détail permis avec les limites physiques de l'appareil . Dans le cas d'un spectre,est la forme spectrale d'une raie très fine. Pour une image il s'agit de l'image d'une source ponctuelle (~patron de diffraction).

3.13 Application de l'analyse de Fourier

voir section 3.14

3.14 Interférométrie (couches minces, Michelson, Young, réseaux)

Un retard entre deux ondes

Fabry-Perot -> spectroscopie très haute résolution spectrale par transformée de Fourier

Michelson -> spectroscopie par transformée de Fourier

Young -> Long base interferometry (VLA, VLBI (planète), GI2T, interférométrie radar (2 orbites)) -> reconstruction d'image par transformée de Fourier

Couches minces -> filtres interférentiels -> reconstruction de la réponse spectrale par transformée de Fourier

3.15 Battements

Deux ondes de fréquences voisines

3.16 Diffraction et pouvoir de résolution d'un instrument

Lumière qui traverse une ouverture

Le champ électrique créé provenant de la lumière passant à travers une infime partie dy de la fente (ouverture linéaire) de largeur a est donné par:

Le champ total est la somme des éléments de champs (c.-à-d. l'intégrale).

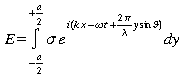
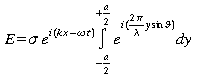
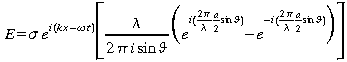
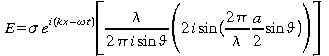
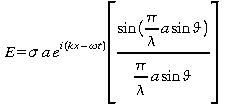
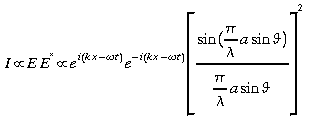
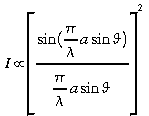
Cette courbe représente la variation de l'intensité lumineuse en fonction de l'angle (ou de la position sur la plan image qui est proportionnel àlorsque les angles sont petits) pour une source d'onde plane passant à travers une ouverture linéaire. Une onde plane peut par exemple être obtenue si nous observons un source ponctuelle (petite taille par rapport à sa distance). Si l'ouverture est circulaire, ce qui est le cas de la plupart des appareils optiques, il faut intégrer le champ d'une série d'ouvertures linéaires d'épaisseur dy et dont la longueur a varie selon l'équation d'un cercle.

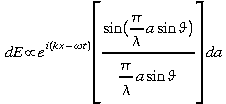
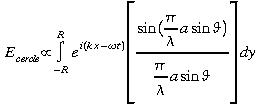et(voir exercice ci-dessous)

Si vous observez simultanément deux sources ponctuelles séparées d'un angle de sorte que vous soyez à la limite de séparabilité des deux images, vous venez de trouver la limite de résolution d'un appareil optique qui est donnée par le critère de Rayleigh. Cette condition est atteinte lorsque le premier minimum de la fonction d'intensité de la première source se superpose au maximum de la fonction d'intensité. La limite de résolution est donnée par:

pour une ouverture linéaire

pour une ouverture circulaire

Exercices 1:

On veut mettre au point un capteur satellitaire qui permet de distinguer, inventorier et dénombrer les différentes espèces de baleines dans l'océan. Si le satellite fonctionne dans le visible () et que la hauteur de l'orbite par rapport au sol est de 200 km, déterminez le diamètre minimal de l'ouverture du télescope qui permettrait de réaliser cette étude. Supposez que pour différencier deux espèces de baleines, le plus fin détail perceptible sur votre image doit être de 25 cm. Discutez votre résultat en fonction des contraintes fixées par la taille des lanceurs orbitaux. Que pouvez vous changer à ce système pour en réduire la taille sans pour autant nuire à ses capacités de détection?

Exercice 2:

En utilisant la fonction de l'intensité de diffraction, démontrez que le critère de Rayleigh d'une ouverture linéaire est donné par.

Exercice 3:

Exprimez la dépendance de a en fonction de y pour une ouverture circulaire et résolvez l'intégrale menant à. Calculez la fonction d'intensité correspondant à cette expression de champ électrique. Comparez votre résultat au cas de l'ouverture linéaire.

3.17 Effet Doppler relativiste

Vous avez vu que pour des ondes mécaniques, l'effet Doppler est donné par

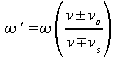
En relativité restreinte, on ne peut distinguer le mouvement de la source et de l'observateur puisqu'il n'y a pas de milieu de référence . Pour l'onde électromagnétique, l'effet Doppler prend la forme:

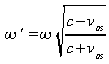cette équation peut être généralisée comme suit

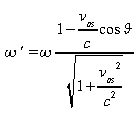où est l'angle entre la vitesse et la direction d'observation

On remarque en particulier que même pour , on observe un effet Doppler relativiste non nul!

Exercice1:

Vous mettez au point un capteur micro-ondes dans le but d'étudier le comportement des animaux en forêt. Pour ce faire vous installez un émetteur de micro-ondes dont la longueur d'onde vaut 1 cm. Vous disposez aussi deux capteurs à micro-ondes. Lorsqu'un animal passe dans le voisinage des capteurs, vous constatez que l'amplitude du signal reçu varie à un rythme de 250 Hz.

Déterminez la vitesse de déplacement de l'animal en supposant que ce dernier réfléchisse les ondes micro-ondes.

Réponse: v_os=5 m/s

3.18 Polarisation de l'onde électromagnétique

La polarisation définie comme l'orientation du vecteur champ électrique de l'onde électromagnétique. Pour de la lumière naturelle comme la lumière solaire, il n'y a pas de direction privilégiée et on dit alors que l'onde est non polarisée. En réalité une onde non polarisée est un mélange d'ondes de toutes les polarisations. L'interaction de l'onde électromagnétique non polarisée avec la matière peut entraîner une polarisation de l'onde nous verrons au dernier chapitre quelques processus conduisant à ce phénomène.

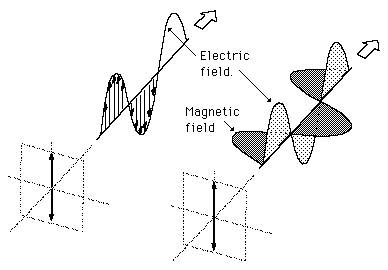
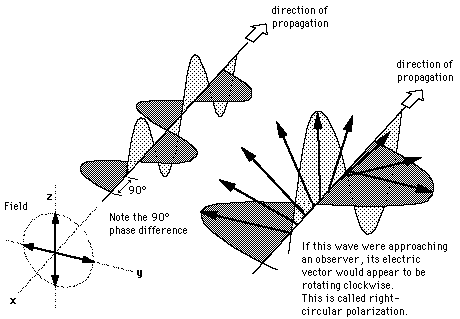
(a) (b)

(a) polarisation linéaire et (b)polarisation circulaire

Polarisation circulaire:

Si l'une des composantes perpendiculaires de l'onde est retardée de 1/4 de longueur d'onde, le vecteur champ électrique semblera tourner. Il s'agit de la polarisation circulaire. Ce dernier est en fait un cas particulier de la polarisation elliptique qui correspond à la situation où l'amplitude des deux polarisation perpendiculaires sont identiques. Les milieux qui permettent un retard différent en fonction de la direction de polarisation sont nommés matériaux biréfringents.

Considérons le cas du retard de 1/4 longueur d'onde entre deux composantes de polarisation perpendiculaires ayant la même grandeur:.

Le vecteur champ électrique résultant peut être exprimé comme suit:

Ce qui permet de calculer l'angle de la polarisation:

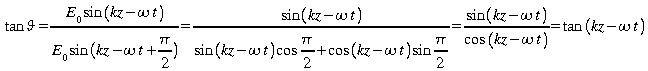
Comme l'angle varie en fonction du temps et de la position (vecteur E est tournant), on parle de polarisation circulaire ou elliptique.