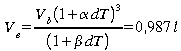Chapitre
2: Notions de thermodynamique
Principes de la thermodynamique
Équilibre thermique: corps A:
T=TA=TC du corps C et si TB=TC
alors TA=TC
Conservation de l'énergie
Entropie d'un système augmente
(processus irréversibles)
Entropie tend vers 0 lorsque T tend vers 0
Concept
de température
Notion intuitive de la température
Exemples déroutants (tige fer vs
bois, poignée de poêle à bois argentée vs
noire, tuiles de la navette spatiale, couronne solaire, marche sur
des tisons ardents, facteur de refroidissement éolien).
Unités: Kelvin 0=-273,3 oC
En fait T représente l'énergie
interne (Unités= joule)
T=0 => aucune énergie interne
(solide inerte)
Profil de température dans
l'atmosphère
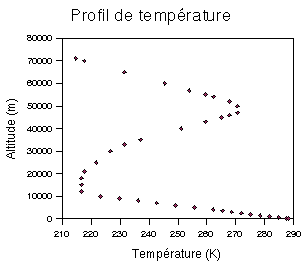
Couche planétaire limite 0-2 km
c'est la plus basse partie de la troposphère où la
majorité des perturbations météorologiques ont
lieux
Troposphère 0-12 km (variable selon
la latitude < aux pôles , 8km alors que 17 km à
l'équateur
T -> -57 oC
Stratosphère 12-45 km T = -57 à
0 oC
chauffage provient de la réaction
O2 -> O3 stimulé par les UV solaires
Couche d'ozone à ~25 km
Mésosphère 45-85 km, T=0 à
-100 oC, densité très faible
Thermosphère T augmente à
nouveau, atomes ionisés par les UV énergétiques
qui sont à l'origine de l'augmentation de la T.
Fusionnée au vent solaire ->
aurores boréales
2.2
Masse volumique
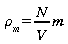
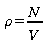 est
la concentration (nombre de particules par mètre cube)
est
la concentration (nombre de particules par mètre cube)
Quelques
valeurs:
|
Substance
|
Condition
|
Masse volumique
(kg/m3)
|
référence
|
|
Air
|
20 oC
|
1,2
|
Arya, 1988
|
|
eau
|
20 oC
|
1000
|
Arya, 1988
|
|
glace
|
0 oC
|
917
|
Arya, 1988
|
|
neige
|
fraîche
|
100
|
Arya, 1988
|
|
sol sableux (40% espace poral)
|
sec
|
1600
|
Arya, 1988
|
|
sol sableux (40% espace poral)
|
saturé
|
2000
|
Arya, 1988
|
|
sol argileux (40% espace poral)
|
sec
|
1600
|
Arya, 1988
|
|
sol argileux (40% espace poral)
|
saturé
|
2000
|
Arya, 1988
|
|
Sol tourbière (80% espace poral)
|
sec
|
300
|
Arya, 1988
|
|
Sol tourbière (80% espace poral)
|
saturé
|
1100
|
Arya, 1988
|
2.3
Concept de pression
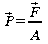
Force par unité de surface
Unités Pascal=N/m2 = kg
m-1 s-2
Travail en thermodynamique
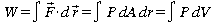 (Unités=joule)
(Unités=joule)
Origine de la pression sous l'eau
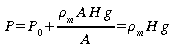 i.e.
1 atm à chaque 10m
i.e.
1 atm à chaque 10m
Origine de la pression atmosphérique
Si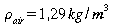 ,
calculer la hauteur de la colonne nécessaire pour générer
une pression de 101 kPa
,
calculer la hauteur de la colonne nécessaire pour générer
une pression de 101 kPa
Profil de densité et de pression
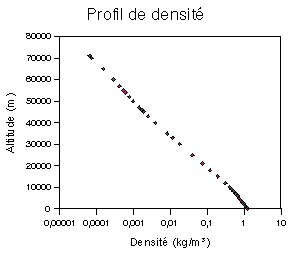
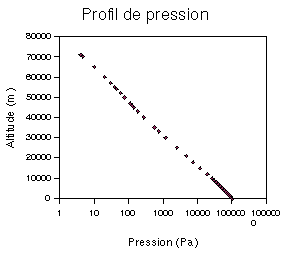
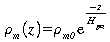 =>
décroît de e à tous les 8 km
=>
décroît de e à tous les 8 km
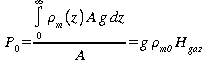
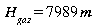
99% de la masse de gaz dans les 30
premiers km
La composition chimique de l'air sec de la
troposphère et de la stratosphère demeure à peu
près fixe en fonction de l'altitude en raison du brassage
occasionné par les mouvement convectifs verticaux. Il est
constitué de 78% d'azote et 21% d'oxygène en volume.
La vapeur d'eau, l'ozone et le CO2
constituent les gaz à grande variabilité. Bien que
leur concentration est faible (~1% du volume) il jouent un rôle
crucial dans l'équilibre radiatif de l'atmosphère car
ils sont hautement absorbants.
2.4
Conduction et résistance thermique
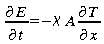
x représente la direction perpendiculaire au flux
d'énergie de sorte que
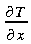 représente
le gradient de température. En réalité le
gradient s'exprime de la façon suivante en 3 dimensions
représente
le gradient de température. En réalité le
gradient s'exprime de la façon suivante en 3 dimensions
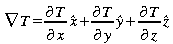
Le gradient est une quantité
vectorielle qui indique toujours la direction de changement maximal
de la variable considérée en fonction de la position.
On peut définir le rapport de
l'épaisseur du matériaux conducteur sur la conductivité
comme étant la résistance thermique R.
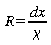
Ce qui permet de réécrire
l'équation de transfert par conduction comme
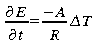
Ce concept est très utile dans
l'industrie car il est possible de définir une valeur de R
pour chaque type de matériau d'épaisseur donnée
et nous pouvons aisément obtenir la résistance
thermique d'une épaisseur quelconque du même matériau
par simple proportion car R est proportionnel à l'épaisseur
du matériau. Pour travailler dans les unités SI il
faudra multiplier la valeur R anglaise par environ 0,17.
|
Substance
|
Condition
|
conductivité thermique
(W/m/K)
|
référence
|
|
Air
|
20 oC
|
0,026
|
Arya, 1988
|
|
eau
|
20 oC
|
0,58
|
Arya, 1988
|
|
glace
|
0 oC
|
2,24
|
Arya, 1988
|
|
neige
|
fraîche
|
0,08
|
Arya, 1988
|
|
sol sableux (40% espace poral)
|
sec
|
0,30
|
Arya, 1988
|
|
sol sableux (40% espace poral)
|
saturé
|
2,20
|
Arya, 1988
|
|
sol argileux (40% espace poral)
|
sec
|
0,25
|
Arya, 1988
|
|
sol argileux (40% espace poral)
|
saturé
|
1,58
|
Arya, 1988
|
|
Sol tourbière (80% espace poral)
|
sec
|
0,06
|
Arya, 1988
|
|
Sol tourbière (80% espace poral)
|
saturé
|
0,50
|
Arya, 1988
|
Ex.
1: calculer la température d'équilibre dans un igloo
hémisphérique de 3 m de diamètre et dont les
parois ont 30 cm de glace et 10 cm de neige. Supposez une
température extérieure de -30 oC et que le
seule source de chauffage est la chaleur dégagée par
6 personnes (75 W par personnes) . On suppose qu'il n'y a pas de
conduction par le sol (i.e. le sol est à la même T que
l'air intérieur ou que le sol est très isolé).
ex.
2: Calcul transfert d'énergie par conduction entre l'air et
le sol (sablonneux sec) en juin dans l'hémisphère
Nord.

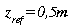
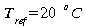
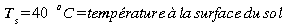
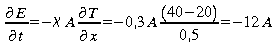
si
nous considérons une surface de 1 m2 alors
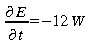
En
fait si on considère que le sol est soumis à des
variations cycliques de la température de surface, il est
possible de modéliser la pénétration de cette
« onde thermique à l'intérieur du sol »
et on en déduit la profondeur d'amortissement zd.
À cette profondeur la variation cyclique de T est atténuée
par le facteur 1/e = 0,37, à 2 zd par un
facteur 0,14 et à 4 zd par un facteur
0,02. Nous pouvons alors considérer qu'à 4 zd
, la température est à peu près constante et
égale à la température moyenne du cycle (le
cycle annuel est considéré ici). Pour les différents
types et conditions de sols caractérisés plus haut,
la profondeur d'amortissement annuelle est de l'ordre de 1.5 m.
Nous pouvons donc considérer la T de la profondeur de 6 m
comme à peu près constante et égale à
la température annuelle moyenne au sol.
Si
on considère que la température de surface varie de
la façon suivante
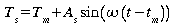 où
Tm=température moyenne de la surface,
As=amplitude de la variation de température,
où
Tm=température moyenne de la surface,
As=amplitude de la variation de température,
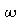 =fréquence
angulaire de la variation cyclique, tm= instant
de la journée où Ts=Tm,
=fréquence
angulaire de la variation cyclique, tm= instant
de la journée où Ts=Tm,
Nous
pouvons montrer que la température à une profondeur z
quelconque est donnée par:
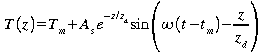
2.5
Équation d'état et loi des gaz parfaits
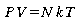
2.6
Chaleur spécifique
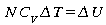
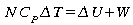
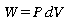
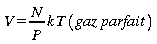
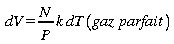
en combinant les deux définitions de
Cp et Cv données ci-haut,
et cette dernière équation on peut démontrer la
relation entre les chaleurs spécifiques et k.
|
Substance
|
Condition
|
Chaleur spécifique
(J/kg/K)
|
référence
|
|
Air
|
20 oC
|
1000
|
Arya, 1988
|
|
eau
|
20 oC
|
4190
|
Arya, 1988
|
|
glace
|
0 oC
|
2100
|
Arya, 1988
|
|
glace
|
-10 oC
|
2100
|
Benson, 2004
|
|
neige
|
fraîche
|
2090
|
Arya, 1988
|
|
sol sableux (40% espace poral)
|
sec
|
800
|
Arya, 1988
|
|
sol sableux (40% espace poral)
|
saturé
|
1480
|
Arya, 1988
|
|
sol argileux (40% espace poral)
|
sec
|
890
|
Arya, 1988
|
|
sol argileux (40% espace poral)
|
saturé
|
1550
|
Arya, 1988
|
|
Sol tourbière (80% espace poral)
|
sec
|
1920
|
Arya, 1988
|
|
Sol tourbière (80% espace poral)
|
saturé
|
3650
|
Arya, 1988
|
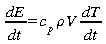
2.7
Théorème d'équipartition de l'énergie
Voir document « théorie
cinétique »
2.8
Distribution de Maxwell-Boltzmann
Voir document « théorie
cinétique » Refroidissement vs
évaporation
2.9
Organisation et entropie maximale
entropie est inversement liée au
niveau de complexité ou d'organisation d'un système
sur le plan microscopique on le calcule
comme le nombre de dégénérescence d'un état
d'énergie (combien de configurations conduisent à la
même valeur de E?)
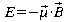
Ex. 4 particules identiques de spin 1/2
dans un champ magnétique
Le phénomène est plus
tranché pour un plus grand nombre de particules.
tendance vers une diminution de l'ordre
Un lien avec la vitesse évolutive
(surfusion, étoiles et galaxies)
revenir sur la notion d'irréversibilité
(pas une règle stricte mais simplement une question de
statistique)
2.10 Changement de phase
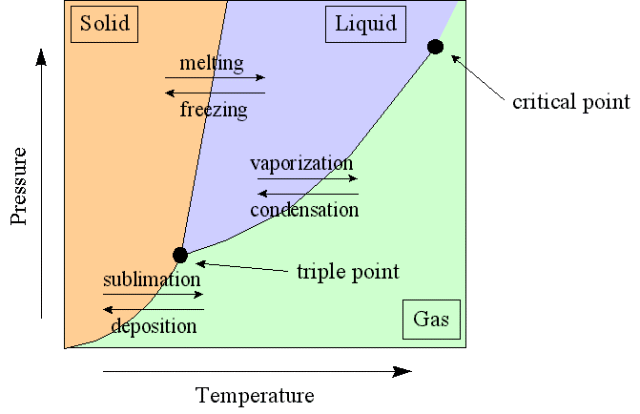
2.11 Chaleur latente
-
|
Substance
|
Lf (fusion)
kJ/kg
|
Lv (vaporisation)
kJ/kg
|
|
eau
|
334
|
2260
|
Ces valeurs
dépendent de la pression à laquelle se produit le
changement de phase
2.12
Chaleur de vaporisation (évapotranspiration)
Comme
pour se vaporiser, l'eau requiert une quantité d'énergie
par unité de masse (chaleur latente), nous pouvons comme nous
l'avons vu à la section précédente déterminer
la puissance transmise par ce processus. Toutefois cette
détermination passe nécessairement par la détermination
du flux massique dm/dt. Ce flux dépend d'un certain nombre de
paramètres dont les conditions atmosphériques (humidité
relative, vent). De plus la géométrie du couvert
végétal (ou plutôt la géométrie du
relief) influence le taux de vaporisation puisque cette dernière
perturbe les conditions atmosphérique à la proximité
de la surface sans oublier qu'elle est intimement liée à
la surface évaporante disponible. Toutefois il est évident
qu'il faut en plus tenir compte d'une certaine résistance de
la surface évaporante ainsi que de son contenu en eau (p. ex.
une plante séchée ne peut pas « évapotranspirer »).
La résistance la plus petite étant celle d'une surface
d'eau libre. En général dans un couvert végétal,
cette résistance est liée aux propriétés
perméables des feuilles.
La
figure ci-dessous illustre les différentes résistances
qui interviennent dans le calcul de dm/dt
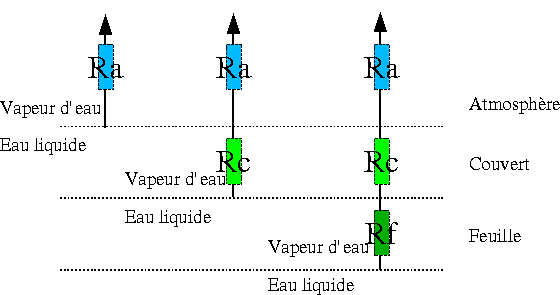
L'approche
que sera préconisée dans ce cours sera l'approche
empirique qui a donné un certain nombre de solution
relativement satisfaisante à ce problème complexe. Les
formules empiriques correspondent généralement à
des moyennes temporelles sur un jour ou quelques années (p.ex.
10 ans) et reposant sur l'étude de couverts végétaux
de type gazon et prairie.
Je
vous propose la formule de Blaney et Criddle:
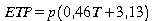 (mm d'eau/jour)
(mm d'eau/jour)
où
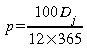 Dj
correspond à la durée du jour en heures
Dj
correspond à la durée du jour en heures
Cette
formule peut être améliorée en introduisant des
coefficients de corrections qui dépendent de la vitesse du
vent et de l'humidité relative.
Pour
une surface d'eau libre (océan) nous pouvons utiliser
l'équation ci-dessous (dérivée par Dalton,
1802!)
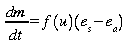 (kg/sec)
(kg/sec)
Le
déficit de saturation représente la quantité
d'eau que l'air peut stocker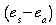 .
es est la pression de vapeur d'eau à
saturation à la température de la surface évaporante,
ea est la pression effective ou actuelle de vapeur
d'eau dans l'air. f(u) est une « constante »
de proportionnalité qui dépend de la vitesse du vent à
la surface. es peut être calculée à
l'aide de la formule de Alt
(1978).
.
es est la pression de vapeur d'eau à
saturation à la température de la surface évaporante,
ea est la pression effective ou actuelle de vapeur
d'eau dans l'air. f(u) est une « constante »
de proportionnalité qui dépend de la vitesse du vent à
la surface. es peut être calculée à
l'aide de la formule de Alt
(1978).
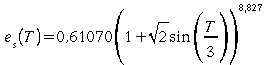 T
est exprimé en oC
T
est exprimé en oC
Cette
pression est calculée en kPa.
ea peut
être calculé à partir de la valeur locale de
l'humidité relative (Hr).
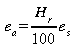
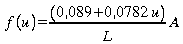 (ASHRAE,
1995) où A est la surface (m2), u est la
vitesse du vent en m/s et L la chaleur latente de vaporisation
de l'eau (kJ/kg). Il est important de noter que la pression de vapeur
doit être mesurée en kPa pour que cette équation
s'applique.
(ASHRAE,
1995) où A est la surface (m2), u est la
vitesse du vent en m/s et L la chaleur latente de vaporisation
de l'eau (kJ/kg). Il est important de noter que la pression de vapeur
doit être mesurée en kPa pour que cette équation
s'applique.
2.13
Dilatation thermique
Joints
de dilatation (ponts, bâtiments)
ex.:
On vous demande de remplir une bouteille cubique (10 x 10 x 10 cm)
de 1 litre d'eau à 20 oC à sa capacité
maximale de façon à que qu'une fois sellée
cette dernière puisse être transportée dans un
environnement à 90 oC sans qu'elle ne risque
d'éclater. Le coefficient de dilatation linéique du
verre est 9x10-6 K-1 alors que le coefficient
de dilatation volumique de l'eau est de 2,1x10-4 K-1
Le volume de la bouteille va augmenter
comme
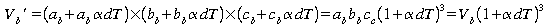 alors
que le volume d'eau va augmenter comme
alors
que le volume d'eau va augmenter comme
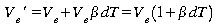
La solution est
trouvée pour
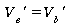
soit
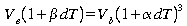
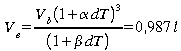
2.14
Convection
libre,
forcée, mixte
Forme
générale
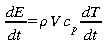
Approche
empirique difficile de déterminer
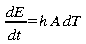 où
h [W/m2/K] est le coefficient surfacique de
convection. Ce dernier peut être calculé à
partir du nombre adimensionnel de Nusselt (qui est la rapport du
flux convectif sur le flux conductif dans les mêmes
conditions)
où
h [W/m2/K] est le coefficient surfacique de
convection. Ce dernier peut être calculé à
partir du nombre adimensionnel de Nusselt (qui est la rapport du
flux convectif sur le flux conductif dans les mêmes
conditions)
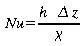
h
dépend de la vitesse du vent, du type d'écoulement
(laminaire ou turbulent), de la rugosité de la surface, et
légèrement de dT. dT représente
la différence de température entre la surface et
l'air.
Nous
le considérerons constant. Gartland and Winkelmann (2001) ont
mesuré une valeur de l'ordre de 5 à 10 au-dessus de
toitures plates.
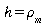



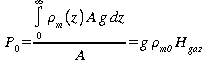
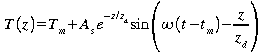
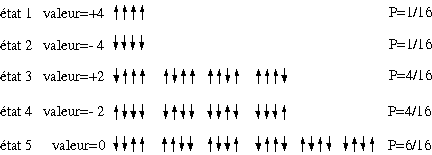


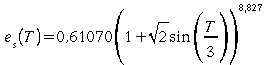 T
est exprimé en oC
T
est exprimé en oC